Embodied cognition, blackboards, and mathematical insight
How we think with things, example one zillion
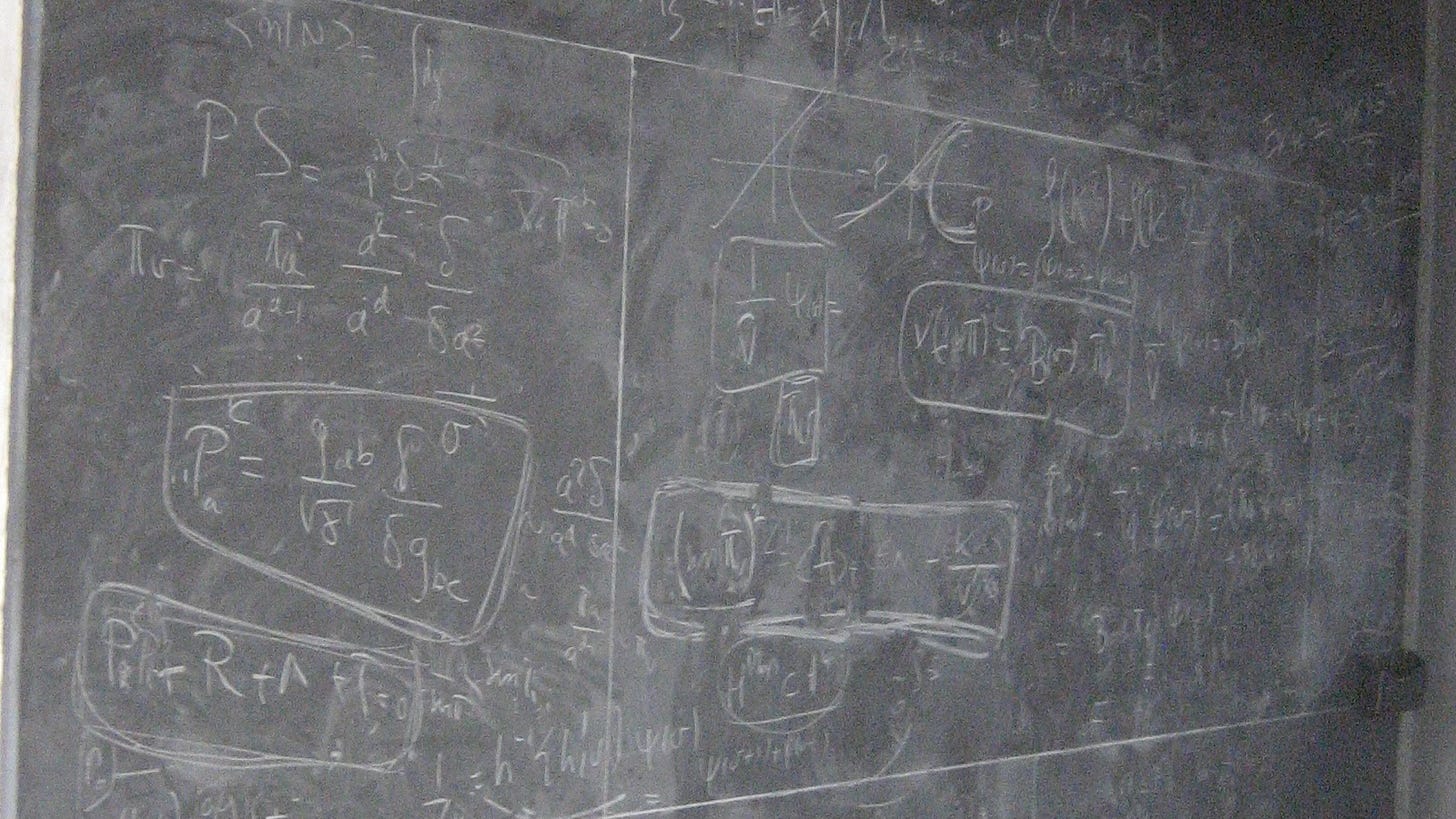
Now and then you come across a body of work that resonates really strongly with your own varied interests. This week I discovered the work of psychologist Shadab Tabatabaeian, a cognitive and information sciences Ph.D. from UC Merced and now postdoc at Georgetown, who studies embodied cognition in mathematics. I was blown away.
Tabatabaeian’s work (published with a small circle of coauthors) asks a deceptively simple question: Why do mathematicians work at blackboards?
Mathematics is all about concepts, logic, proofs, and other things that are abstract and cerebral; and so if any kind of knowledge work could happen independent of place, it would be math. Tabatabaeian's work starts wth a bold claim that this vision is backwards-- or at least highly incomplete. “Despite mathematics’ reputation for silent reflection,” Tabatabaeian writes in one article, in reality “its practice is almost always a form of manual labor — scribbling, sketching, erasing, gesturing.” Indeed, as she puts it in another article, when you watch how they work, “mathematical practice appears to be a species of physical labor.”
That labor happens mainly at blackboards, and the practice is widespread enough for mathematicians to even talk about a specific brand of chalk— Hagoromo's Fulltouch— the way pianists talk about Steinway. “Real-world mathematical cognition involves a lot of writing,” Tabatabaeian writes in one article.
Blackboards aren’t just convenient but ultimately disposable props for mathematicians: their work “occurs within a distributed system that often includes—in addition to a mathematician’s brain—their body, a blackboard or notepad, and the inscriptions they create.” To put it another way, mathematicians think with blackboards, in somewhat the same way that musicians and instruments become part of the same expressive system.
That thinking doesn’t just involve standing and writing. “[E]ven when deep in thought, they often remain in constant motion, stepping toward the blackboard to write and then stepping back to inspect their handiwork.” One of the advantages— or to be more technical, affordances— that blackboards have over sheets of notebook-sized paper is sheer size. A blackboard lets you write a lot of stuff, then step back and survey what you’ve written. For mathematicians, the blackboard and surrounding workspace becomes like “an ecosystem, with mathematicians actively constructing their own ‘notational niches’ within which they can reason by inscribing (e.g., sketching, writing, erasing), gesturing (e.g., pointing to connect two inscriptions), and looking (e.g., shifting gaze from one inscription to another).”
That blackboards are closely linked with cognition is not a new idea. An 1880 sales catalog (as Christopher Philips notes) described the blackboard as “mirror reflecting the workings, character, and quality of the individual mind.”
Notice that the work of thinking through problems doesn’t just happen in the form of writing: one of the important things I take away from Tabatabaeian’s work is that physical activity— the gesturing, looking around at different parts of the blackboard, pointing here and there to identify a new connection— is part of mathematical thinking. Mathematicians don’t just think with symbols and their brains; they think using their bodies, too.
This parallels a study I did a few years ago about “paper spaces” and their role in futures thinking.
Scenario planning workshops involving corporate groups— product developers, strategists, executives, etc.— are often organized into working sessions that involve brainstorming ideas, writing them on Post-Its, and then putting them on blackboard-sized sheets of paper. Working this way allows groups to easily share ideas, move them around in thought experiments, explore new connections between them and imagine various possible futures: the Post-its become immutable mobiles (to borrow from Bruno Latour), and the big paper becomes a space where participants can store, manipulate, and generate new ideas. They encourage participants to think big.
Tabatabaeian then goes on in her latest article to do something really interesting: she looks more closely at how movement around a blackboard reflects different stages in mathematicians’ problem-solving. Writing, stepping back, looking around, pointing at different places may look at first like “aimless wandering,” but she argues that it’s not. “Movement changes the information that is visually accessible, and this change in visual information can hint at unexpected connections.” As with paper spaces, blackboards let you zoom in on details and zoom out to see the big picture, and you do that by physically moving around. And if you watch carefully, you can literally see when mathematicians have found a solution to a problem by how they move.
A century ago, Graham Wallas proposed a four-stage model of creative problem-solving that we still use today (though tragically Wallas himself is all but forgotten). When we work on solving ideas, he argued, we go through
Preparation-- the conscious work of identifying a problem, sketching it out, assembling evidence, etc;
Incubation-- a period of subconscious reflection an exploration;
Illumination-- the "a-ha" moment where suddenly (It feels) we see the answer;
Verification-- the follow-up work of proving that the insight stands up.
That third stage is the one that everyone's really interested in, because it feels so mysterious and elusive-- and so satisfying when it happens.
The question that Tabatabaeian asks is this: if the embodied cognition thesis is right that our bodies and tools play a role in shaping how we think, and when we work we create a knowledge ecosystem, are Wallas' stages visible in how mathematicians work? Further, if you take the ecosystem metaphor seriously, can you use mathematical models of ecological systems to explain what's happening? As Tabatabaeian puts it, "If mathematical insights are critical transitions within this distributed system of mathematical activity, then they should be anticipated by signals that the system’s current regime is no longer stable or resilient." You should be able to see the system shifting when insights appear.
She set up an experiment in which she videotaped mathematicians working in their offices on problems from the William Lowell Putnam Mathematical Competition. This is a competition featuring what everyone recognizes as an extremely challenging set of problems, and even academic mathematicians need time to work through them.
What she found was that in the preparation phase, mathematicians would spend a few minutes writing on the board. Not surprising. At a certain point they shift from mainly writing, to standing back a bit-- close enough to still annotate the board but far enough to see more of the board and equations that are some distance apart. Video showed them concentrating their attention on a couple areas, reflecting the reasoning they were trying to use to solve the problem.
But then you see something really interesting: "their blackboard interactions (e.g., writing, gesturing) became increasingly unpredictable before an insight, analogous to the critical fluctuations that anticipate transitions in physical and ecological systems.”
This process of behavioral destabilization [i.e. looking at new areas of the blackboard, stepping away from their previous location to a new position] began minutes before the insight occurred.... Mathematicians’ situated activity became increasingly unpredictable in the lead up to a sudden insight, starting more than two minutes before they expressed an insight.... Surprisal [i.e., novel movement, looking at different parts of the board than they had before, gesturing to different things] ramped up gradually in the minutes before the insight, peaked after the moment of insight, and then decreased precipitously.
For someone familiar with the literature on the psychology of creativity, and the embodied cognition literature, this is utterly fascinating material, and a wonderfully elegant evidence in favor of Wallas' model and the embodied nature of knowledge. And even if you're not, I think we've all had the experience of working on a problem, and feeling that physical agitation that comes when a novel idea appears, or of spotting a connection between ideas you've written at different times.
Tabatabaeian's work tells us that this isn't just epiphenomenal froth, or relief at solving a difficult problem; it's part of the process of working to a solution. Or as she puts it, “Even at the pinnacle of abstraction, at the highest levels of expertise, new ideas are born when the body discovers unexpected affinities among ideas.”
It makes me wonder whether you can see the impact of the blackboard in the history of mathematics, or in other disciplines. Blackboards are introduced in the early 19th century, and if there is a burst of creativity in the discipline, a growing complexity in mathematical proofs, an increase in the number of collaborative projects and publications, or some other development that could be connected to changes in practice and thinking in this new ecosystem, that would be highly suggestive. (This also reminds me of Paul Saenger's work on word spacing and shifts in scholarly writing and practice.)
There are also some suggestions that the blackboard enabled users to do their work in public in a way that could be energizing. Michael J. Barany and Donald Mackenzie open their article on blackboards and materials in mathematics with this quote about nineteenth-century mathematician Augustin-Louis Cauchy:
Chalk in hand, his formulas expressed themselves, it seems, more easily on the board than they were able to with pen in his note- books, for in his listeners’ presence his fecund genius found again a new zeal, and a ray of joy illuminated the lines of his face when the proof he sought to render understandable struck his audience with obviousness.
You could also make some responsible inferences about the importance of blackboards and how people used them from office layouts. Setting up a blackboard behind your desk, where only you could reach it, would signal a somewhat different practice than having it in a more accessible part of your office, where you and colleagues could stand and work together. I'm not sure how many such diagrams or student recollections survive, but I'll bet there are some.
Though blackboards weren't just confined to offices. In a lovely illustration of how important blackboards are to mathematical thinking and problem-solving, the great mathematician David Hilbert set one up in his garden. His student Richard Courant reported, "He spent his whole time gardening and in between gardening and little chores, he went to a long blackboard, maybe twenty feet long, covered so that also in the rain he could walk up and down, doing his mathematics in between digging some flower beds.”
As a math PhD student, I found this really interesting! Thank you :)
I love the insights that the embodied cognition offers into how our minds may work. This thoughtful article makes me wonder how writers can best approach their task: an effectively linear screen doesn't seem right, and I've never warmed to Scrivener.